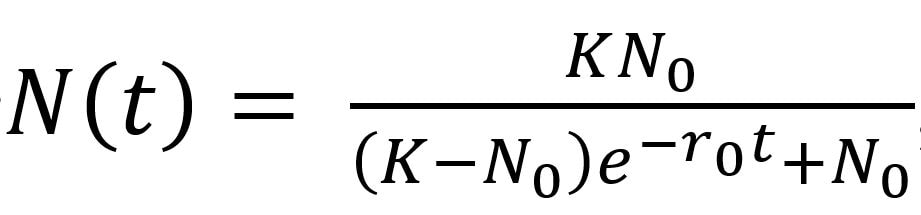June 11th, 2017

In ecology, the understanding of fluctuations in abundances of organisms’ forms the foundational building blocks of population models.  One of the most fundamental models for population growth is the logistic growth model (above),  where the number of individuals at time t: N(t) is a function of the number of individuals at the previous time-step (N sub 0), the carrying capacity (K), and the intrinsic rate of increase, (r sub 0, referred to as r not). [Note e the base of the natural logarithm, aka Euler's constant ~ 2.718]. Sibly et al. (2005) made a major contribution to the rich field of population ecology when they analyzed 1780 time series of population dynamics from 647 taxa, including insect, fish, bird, and mammal species.  They were mainly interested in the relationship between population growth rate (pgr);  and population size (N), or the manner/speed with which pgr slows as a population reaches carrying capacity (K).  Based on the data, they concluded that they could ‘rule out the possibility that the shape of the pgr-density relationship is strongly associated with taxonomy or body size’.  By analyzing the curvature of the pgr-density relationship (i.e., whether shape of the curve was convex or concave), they qualitatively classified the relative rates (or negative slope) at which populations reached carrying capacity into three classes (basically, fast – convex, where θ < 1; slow – concave, where θ > 1, or constant (i.e., linear), where θ ≈ 1).  They then analyzed frequencies of θ, finding that many of the time-series had more frequent negative values for θ, concluding that the majority of populations for the 647 taxa analyzed were ‘living at densities above the carrying capacity of their environments.’
            These conclusions, along their analytical approach, sparked quite a stir in the field population ecology, inciting at least 3 responses.  Reynolds and Freckleton (2005) point out that there may be high degrees of measurement errors, because the time series used in the analyses use estimates of population numbers rather than direct counts.  They contend that it is unclear how θ (pgr in relation to population density) behaves when there are measurement errors, or when density dependence is weak or absent.  Additionally, θ values less than 1 violate one of the primary assumptions of the logistic growth mode: the assumption that density dependence is linear with increasing population size (N).  Reynolds and Freckleton rephrase the conclusions of Sibley et al. to point out that concave population growth rates signify that population decline to carrying capacity is slower than population growth rates are when approaching carrying capacity, a conclusion with implications for management of organismal populations (e.g., fisheries or wildlife). 
            Seven months later, two additional replies to Sibley et al. were published in the same issue of Science.  Joshua V. Ross (2006) pointed out that Sibley et al. failed to note that negative values of θ do not make much sense biologically, and that θ should be constrained to positive values.  Ross clearly explains the math, in that if you take limit of pgr to negative infinity, population size (N) approaches 0 (i.e., extinction), when θ<0 and >0.  Ross revisits the shape of the pgr-density cures, showing population growth to be concave when less than -1 but greater than zero, and convex when greater than 1, a very important caveat.  Additionally, C. Patrick Doncaster (2006) addresses the cases where the pgr-density relationship is less than -1.  He eloquently shows graphically, that θ has a strength parameter, γ, that measures the strength of the density dependence (DD).  When DD operates ‘perfectly’ (i.e., is the only regulating force on population growth and returns populations to K), values of γ are equal to 1.  However, when density dependence overcompensates (i.e., regulating populations to numbers below K when N above K), γ values are >1.  The interesting cases arise when density dependence is weak, or γ values are < 1, in that the nature of exponential population growth means that populations spend more time ascending to carrying capacity than they do descending.  This gets to a faulty conclusion of Sibley et al., in that they failed to account for variability in strength of density dependence.  Doncaster concludes that the shape of the pgr-density relationship reveals more about population regulation than it does about θ, largely due to independent stochastic forces on populations (i.e., all pgr-density relationships become concave when accounting for stochasticity). 
            In this light, I revisit the conclusions of McMahon et al. (2009) in regard to their study of Elephant Seal populations on Marion Island.  Results from the study found θ estimates for the population to be >4 with a pgr-density slope of roughly -1.  McMahon et al. then concluded that there were two distinct phases of population growth, where the population was increasing from 1987-1997, and when the population was decreasing from 1997-2004, and that this was being driven by stochastic changes in the environment associated the Southern Oscillation Index.  Given the information about logistic population growth brought to light by Sibley et al. and their respondents, I suggest that Marion Island seal populations are being regulated by DD.  The two models in the McMahon et al. study found K to be 452 and 483 [breeding female] individuals, and that population was above K from 1986 to 1991.  With a pgr-density curve having a slope of -1, population return to carrying capacity should be constant, unless the strength of the density dependence, γ, increases with population size.  McMahon et al. failed to explore the relationship of γ and N, making it unclear as to whether environmental stochasticity or DD was making the major contribution to regulating Elephant Seal populations.  Elephant Seals are long lived mammals (k-selected organisms), and a time series of 18 years may not be long enough to understand the how the strength of DD in populations scales with the pgr-density curve.  I guess, they will just have to keep counting them to find out.  

References:
Doncaster, C. P. 2006. Comment on" On the regulation of populations of mammals, birds, fish, and insects" III. Science 311:1100-1100.
McMahon, C. R., M. N. Bester, M. A. Hindell, B. W. Brook, and C. J. Bradshaw. 2009. Shifting trends: detecting environmentally mediated regulation in long-lived marine vertebrates using time-series data. Oecologia 159:69-82.
Reynolds, J. D., and R. P. Freckleton. 2005. Population dynamics: growing to extremes. Science 309:567-568.
Ross, J. V. 2006. Comment on" On the regulation of populations of mammals, birds, fish, and insects" II. Science 311:1100-1100.
Sibly, R. M., D. Barker, M. C. Denham, J. Hone, and M. Pagel. 2005. On the regulation of populations of mammals, birds, fish, and insects. Science 309:607-610.